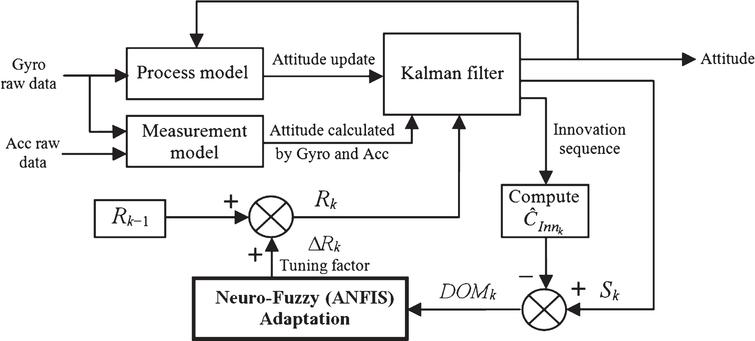
Kalman Filter Auto Tuning
Click Deselect All to cancel selecting all objects on the current tab.Click Options to specify additional settings.
This example shows how to perform Kalman filtering. Both a steady state filter and a time varying filter are designed and simulated below.
- Kalman Filter Auto Tuning Tool
- Extended Kalman Filter
- Extended Kalman Filter Tutorial
- Auto Tuning.ro
- Kalman Filter Examples
Problem Description
System state (Fk, Hk, Qk and Rk) is known, the Kalman filter equations automatically guarantee statistical consistency. However, in many situations the model is not known precisely, and so the filter must be tuned. Filter Tuning Filter tuning is the process of selecting parameters to opti-mize performance. Consistency ensures two desirable. The extended Kalman filter is implemented to online tuning the fuzzy membership function. In fact, EKF estimates the ideal and proper state (MF parameters) for Fuzzy controller based on the current state, current speed error and previous information. Consequently, fuzzy membership functions are. I have to tell you about the Kalman filter, because what it does is pretty damn amazing. Surprisingly few software engineers and scientists seem to know about it, and that makes me sad because it is such a general and powerful tool for combining information in the presence of uncertainty. The Kalman filter deals effectively with the uncertainty due to noisy sensor data and, to some extent, with random external factors. The Kalman filter produces an estimate of the state of the system as an average of the system's predicted state and of the new measurement using a weighted average. The purpose of the weights is that values with. What are the most efficient methods for tuning Kalman Filter process noise covariance matrix, Q? We indicate how some of the well known credibility models may be formulated as Kalman filters.
Given the following discrete plant
where
Kalman Filter Auto Tuning Tool
design a Kalman filter to estimate the output y based on the noisy measurements yv[n] = C x[n] + v[n]
Steady-State Kalman Filter Design
You can use the function KALMAN to design a steady-state Kalman filter. This function determines the optimal steady-state filter gain M based on the process noise covariance Q and the sensor noise covariance R.
First specify the plant + noise model. CAUTION: set the sample time to -1 to mark the plant as discrete.
Extended Kalman Filter
Specify the process noise covariance (Q):
Specify the sensor noise covariance (R):
Now design the steady-state Kalman filter with the equations
The first output of the Kalman filter KALMF is the plant output estimate y_e = Cx[n n], and the remaining outputs are the state estimates. Keep only the first output y_e:
To see how this filter works, generate some data and compare the filtered response with the true plant response:
To simulate the system above, you can generate the response of each part separately or generate both together. To simulate each separately, first use LSIM with the plant and then with the filter. The following example simulates both together.
Next, connect the plant model and the Kalman filter in parallel by specifying u as a shared input:
Finally, connect the plant output yv to the filter input yv. Note: yv is the 4th input of SYS and also its 2nd output:
The resulting simulation model has w,v,u as inputs and y,y_e as outputs:
Extended Kalman Filter Tutorial
You are now ready to simulate the filter behavior. Generate a sinusoidal input vector (known):
Generate process noise and sensor noise vectors:
Now simulate the response using LSIM:
Compare the true response with the filtered response:
As shown in the second plot, the Kalman filter reduces the error y-yv due to measurement noise. To confirm this, compare the error covariances:
Covariance of error before filtering (measurement error):
Auto Tuning.ro
Covariance of error after filtering (estimation error):
Time-Varying Kalman Filter Design
Kalman Filter Examples
Now, design a time-varying Kalman filter to perform the same task. A time-varying Kalman filter can perform well even when the noise covariance is not stationary. However for this example, we will use stationary covariance.
The time varying Kalman filter has the following update equations.
First, generate the noisy plant response:
Next, implement the filter recursions in a FOR loop:
Now, compare the true response with the filtered response:
The time varying filter also estimates the output covariance during the estimation. Plot the output covariance to see if the filter has reached steady state (as we would expect with stationary input noise):
From the covariance plot you can see that the output covariance did reach a steady state in about 5 samples. From then on, the time varying filter has the same performance as the steady state version.
Compare covariance errors:
Covariance of error before filtering (measurement error):
Covariance of error after filtering (estimation error):
By utilizing the propelled source signal division innovation, it gives the recurrence subordinate drum level control that has the range from up to 18dB to improve essentially complete removal.UNMIX DRUMS VST can be utilized for taking care of business and upgrading the effect of the drums in an exceptionally interesting manner. Download umix drums vst. This great sound module opens up some new alternatives for test based music creation. With everything taken into account UNMIX DRUMS VST is an overwhelming application that permits you to help the drums in blended music continuously.UNMIX DRUMS VST is a great module that lets you support the drums in blended music in the constant.
Verify that the steady-state and final values of the Kalman gain matrices coincide: